Regional Days on Model Theory and Applications
6th edition - Düsseldorf, 14th+15th of Feb 2024

Back to the main RDMTA page

Main local organizers: Immi Halupczok, Nadja Hempel
Additional organizers: Florian Felix, Hamed Khalilian, Saba Aliyari

This RDMTA is funded by the DFG, via the GRK 2240.

Schedule

Wednesday 14th:

9:45-10.30	Welcome coffee
10.30-11.30	Silvain Rideau: Multi topological fields, approximations and NTP2
	Abstract ▷ (Joint work with S. Montenegro) The striking resemblance between the behaviour of pseudo-algebraically closed, pseudo real closed and pseudo $p$-adically fields has lead to numerous attempts at describing their properties in a unified manner. In this talk I will present another of these attempts: the class of pseudo-$T$-closed fields, where $T$ is an enriched theory of fields. These fields verify a « local-global » principle with respect to models of $T$ for the existence of points on varieties. Although it very much resembles previous such attempts, our approach is more model theoretic in flavour, both in its presentation and in the results we aim for. The first result I would like to present is an approximation result, generalising a result of Kollar on PAC fields, respectively Johnson on henselian fields. This result can be rephrased as the fact that existential closeness in certain topological enrichments come for free from existential closeness as a field. The second result is a (model theoretic) classification result for bounded pseudo-$T$-closed fields, in the guise of the computation of their burden. One of the striking consequence of these two results is that a bounded perfect PAC field with $n$ independent valuations has burden $n$ and, in particular, is NTP2.
11.40-12.40	Stefan Ludwig: Difference fields with an additive character on the fixed field
	Abstract ▷ Motivated by work of Hrushovski on pseudofinite fields with an additive character we investigate the theory $\operatorname{ACFA}_+$ which is the model companion of the theory of difference fields with an additive character on the fixed field. Building on results by Hrushovski we can recover it as the characteristic 0-asymptotic theory of the algebraic closure of finite fields with the Frobenius-automorphism and the standard character on the fixed field. We characterise 3-amalgamation in $\operatorname{ACFA}_+$ and obtain that $\operatorname{ACFA}_+$ is simple as well as a description of the connected component of the Kim-Pillay group. If time permits we present some results on higher amalgamation.
12.40-14.00	Lunch
14.00-15.00	Florian Felix: Universality of Cluckers-Loeser Motivic Integration
	Abstract ▷ I will give an introduction to the topic of my PhD thesis. Raf Cluckers and Immanuel Halupczok showed that in the case of $p$-adic integration an analogue of the Kontsevich and Zagier period conjecture is true: Equalities between semi-algebraic sets come from a set of very easy transformation rules. While this does not provide an approach to the real case, it naturally leads to the question whether something similar holds in other non-archimedean integration theories. I will give a general (and vague) introduction to motivic integration in the style of Cluckers-Loeser over $K((t))$ for a field $K$ of characeristic 0 using the $p$-adics as a guiding principle to discuss similarities and differences between the $p$-adic case and $K((t))$.
15.10-16.10	Simone Ramello: Valued difference fields: beyond surjectivity
	Abstract ▷ We tackle the problem of axiomatizing theories of valued difference fields in the case where the endomorphism is not surjective, building on previous work of Pal (in the inversive multiplicative case) and Dor-Halevi (in the non-inversive contracting case). We establish the Relative Embedding Property for a natural elementary class of non-inversive multiplicative valued difference fields, and deduce AK/E-style transfer results.
16.10-16.50	Coffee
16.50-17.50	Leon Chini: Model companions of o-minimal theories with a rational vector space homomorphism
	Abstract ▷ Let $T$ be a complete and model-complete first-order theory, which defines a non-trivial rational vector space in every model. Define $T_\theta := T \cup \{\text{“$\theta$ is a homomorphism of said vector space”}\}$. We also consider certain extensions $T^C_\theta$ of $T_\theta$, which enforce that the kernels of some endomorphisms of the form $f[\theta] = \sum_{i=0}^d (f_i) \cdot \theta^i$ satisfy certain equations. I will present a criterion for when these expansions have a model companion. For three special expansions, I will explicitly state a characterization of existentially closed models and show how one uses this condition to make these characterizations first order. By previous work of Block Gorman, said condition holds in certain o-minimal theories, which include $\operatorname{Th}(\mathbb{R}, 0, +, <)$ with the additive group as a vector space and $\operatorname{RCF}$ with the multiplicative group on the positive elements as a vector space. If time permits, I will present some results obtained for the respective model companions in these cases.
19.00	Conference dinner at the Giosy, which is here
	Menu ▷

Thursday 15th:

9.30-10.30	Marco Amelio: Non-split sharply 2-transitive groups in odd characteristic
	Abstract ▷ (joint work with S. André and K. Tent) Until recently, the existence of non-split sharply 2-transitive groups (i.e., sharply 2-transitive groups without a non-trivial normal abelian subgroup) was an open problem. The first examples were produced by Rips, Segev and Tent in 2017 and by Rips and Tent in 2019. It is possible to associate to every sharply 2-transitive group a characteristic, that is either 0 or a positive prime number. The first of these examples have characteristic 2, while the other ones have characteristic 0, leaving the problem open for odd characteristics. In this talk, I will give some background on sharply 2-transitive groups and a rough overview on how we adapted the construction used for characteristic to 0 to odd characteristic, using methods of geometric small cancellation.
10.30-11.10	Coffee
11.10-12.10	Tingxiang Zou: Around the Elekes-Szabó's Theorem
	Abstract ▷ The Elekes-Szabó's Theorem roughly says the following: Let $R$ be an algebraic ternary relation in $W_1\times W_2\times W_3$ defined in a field $K$ of characteristic 0, such that any two coordinate is interalgebraic with the third one, for example the collinear relation for three points in a curve. Suppose there are arbitrarily large finite subsets $X_i$ of $W_i$ with each $X_i$ of size $n$ and has bounded intersection with any subvariety of $W_i$, such that the intersection of $R$ with $X_1\times X_2\times X_3$ has size approximately $n^2$, then $R$ must be essentially the graph of addition of some commutative algebraic group $G$. With Martin Bays and Jan Dobrowolski, we are trying to remove the assumption of having bounded intersection with any subvarieties. This assumption is called in general position. Along the way, we develop a group action version of the Elekes-Szabo's Theorem, which seems necessary if one wants to remove the general position assumption. In this talk, I will give an overview of the Elekes-Szabó's Theorem and the model theoretic approach towards it.
12.40-14.00	Lunch

Confirmed speakers

• Florian Felix (Düsseldorf)
• Leon Chini (Bonn)
• Marco Amelio (Münster)
• Silvain Rideau-Kikuchi (Paris)
• Simone Ramello (Münster)
• Stefan Ludwig (Paris)
• Tingxiang Zou (Münster/Bonn)

Registration

If you want to participate, please register here, preferably on the 05.02.2024 at latest.

For a limited number of young researchers, the hotel rooms can be funded. The application deadline for this is 31.01.2024.

Travel and venue

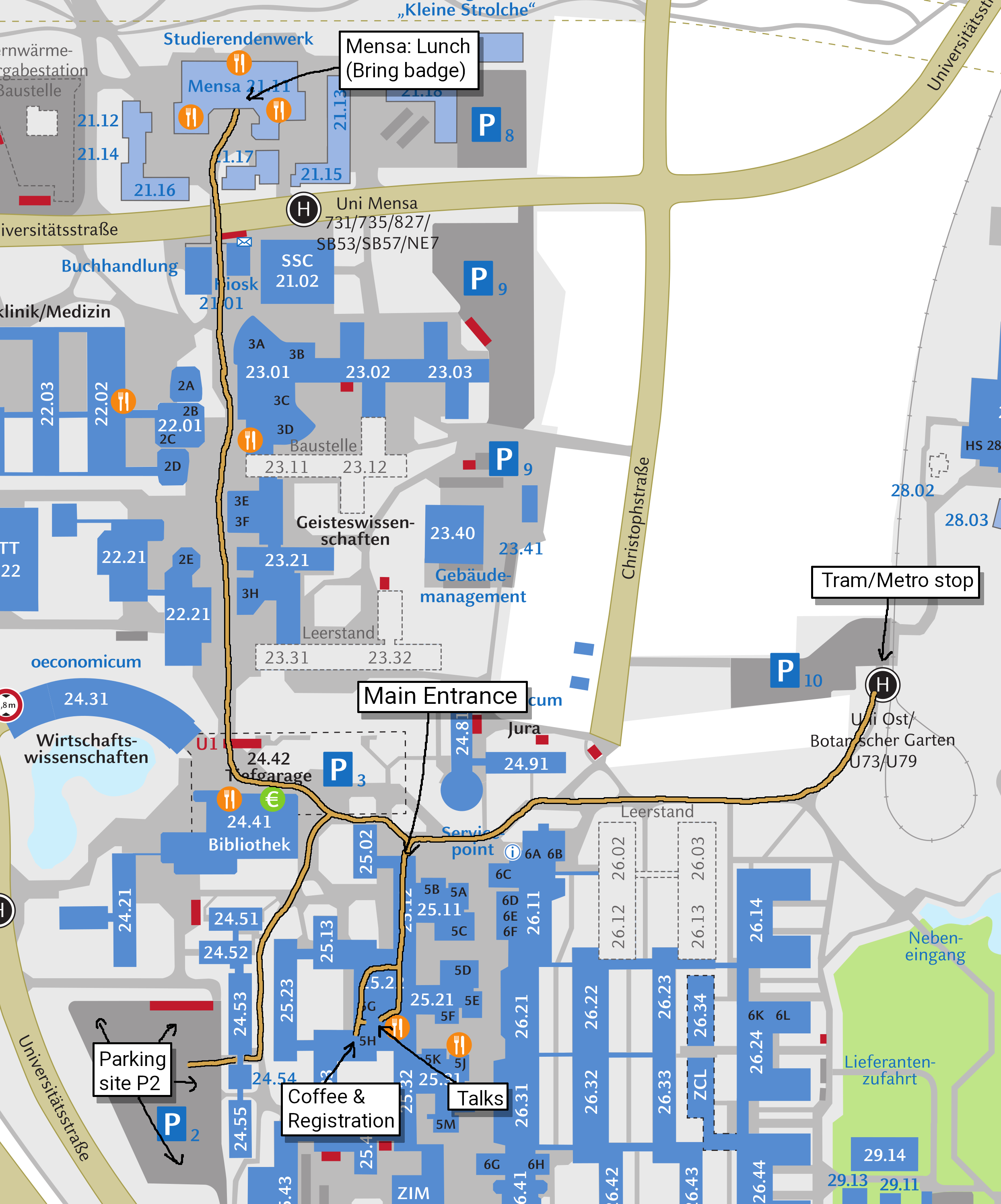
Conference venue:

All talks will take place in lecture hall 5H, in the building 25.22. Coffee and cookies will be served in room 25.22.00.53, which is very close to that lecture hall.

Map ▷

Hotel:

If you do not get the hotel room funded by us, please book a hotel on your own. Speakers will be lodged at the HK-hotel, which is in 25 min walking distance from the venue of the conference. Another nice hotel nearby is Haus Mooren.

Public transport tips:

• To find routes, you can use the website of the Deutsche Bahn or the website of the Verkehrsverbund Rhein-Ruhr. You can also download the DB Navigator app.
• If you travel between Düsseldorf main station, the hotel and the university, you need a ticket Preisstufe A or Preisstufe A3. There are single tickets and tickets valid for several (e.g. 4) trips. If you arrive with a train ticket of the deutsche Bahn which, as destination, says "Düsseldorf+city", then that ticket is valid in the local transports.
• In case you buy a ticket from a ticket vending machine, you might (or might not) need to stamp your ticket using the stamp machines inside the trains/trams/subways.

Arrival by car:

If you arrive by car, we recommend parking on the parking site P2 of the university.